電磁気学⑥　ファラデーの電磁誘導の法則

「電場に関するガウスの法則」と「磁場に関するガウスの法則」は、それぞれ「電場単体」と「磁場単体」の性質を表現したものでした。

電磁気学で扱われる4つの現象は、残り2つですが、その2つは共に「電場と磁場の相互作用」についての実験結果がまとめられています。

ここでは「ファラデーの電磁誘導の法則」を考えます。

この法則は、「磁場が動くと電場が発生する」という現象を表現しています。電と磁が相互作用しています。

現象としては、以下のようなものです。

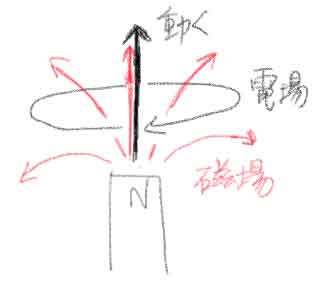
磁石が移動して、空間内の磁場が変化すると、その周辺に「風が吹くように電場が発生」します。図では、黒の太線方向にN極が移動することで、黒の楕円で書いた電場が発生しています。新しく発生した電場を楕円で書いたのは、「理想的な小さいプラスの電荷」を置くと、回るように電場から力を受ける、という現象を表現するためです。

この現象に対応する式は、以前紹介した、

\( \displaystyle \nabla \times \boldsymbol{E} = -\frac{\partial \boldsymbol{B} }{\partial t} \)

です。

右辺の

\( \displaystyle -\frac{\partial \boldsymbol{B} }{\partial t} \)

が「磁場が動くと」に相当します。「動く」というのは「時間変化する」という意味で、磁場に関する物理量（磁束密度 \( \boldsymbol{B} \) ）の時間微分になっています。

また、左辺の

\( \nabla \times \)

の部分は「ローテーション」とよばれる演算の記号で、「回転」現象を表現しています。
\( \nabla \times \boldsymbol{E} \)と書くことにより、「風が吹くように発生した電場」を表現しています。

ところで、時間変化する磁場は電場を発生させるわけですが、磁場も保持しています。上の図の赤線は「磁場」です。