の話。
\( \nabla \cdot \) は「ダイバージェンス」とよばれる演算の記号で、「発散」とか「湧き出し」を表現しています。
そのため、
\( \displaystyle \nabla \cdot \boldsymbol{D} \)は「電場が湧き出す現象」を表現しています。電場は電荷によって発生すると思われているので、以下のようなイメージの数学的表現です。
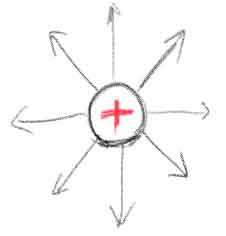
「湧き出し」は負の場合、「吸い込み」になります。電場はプラスの電荷から湧き出し、マイナスの電荷に吸い込まれます。
…ガウスの法則が表現しているのは…それだけです。シンプルでよいのですが、このままだとあまり実用的ではないので、関連する現象も考えます。
電気現象で問題になるのは、電場そのものではなく、電気力です。人間には電場そのものを知覚する能力はありませんので、実際に観察できるのは、電気力によって、電荷や光が力を受けて移動する現象です。
現在の科学では「なぜ電気力が発生するのか」については分かっていませんので、実験結果だけを数学的に表現して満足することにします。電気力の実験結果は以下の2つです。
1.電気力は電荷の大きさに比例する。
2.電気力は電荷間の距離により急激に小さくなる。
「急激に」というのは二乗分の1で減少する、という意味です。つまり、数学的な表現では
\( F \propto q_0 \times q_1 \)
\( F \propto r^{-2} \)
となります。ここで、\( \propto \) は「比例」を表す数学的な記号です。これをまとめて1つの式で表現します。それが「電気力に関するクーロンの法則」で
\( \displaystyle F= k \frac{q_0 q_1}{r^2} \)となります。ここで、\( F \) が電気力、\( q_0 \) と \( q_1 \) が2つの電荷の「電荷の大きさ」、\( r \) が電荷間の距離です。
1つにまとめるとき、比例記号 \( \propto \) から等式 \( = \) に変更しているので、比例係数として \( k \) を導入しています。この比例係数を「電気力に関するクーロン定数」とよびます。
この形式の式は「電気力の大きさ」だけを表す表現なので、力の向きは別に考えます。力の向きは電荷の符号に依存し、同符号なら斥力、異符号なら引力です。
クーロンの法則も「なぜ電気力は発生するか」の解釈は示していません。あくまで、実験結果を数学的に表現しただけです。
「電気力」の性質と、それを数式で書く過程は、「重力」を数学的な表現で記述したときと非常に似ています。そのため、重力と電気力(磁気力もですが)には何らかの関連があるのではないかと興味を持つ人も多く、研究は続けられてます。


コメント