高校物理では、エントロピーという物理量は出てきません。
エントロピーは「説明しにくい物理量」だからです。しかし、エントロピーも大切な物理量のひとつです。高校までの物理を学んでいる方も、学校で習わないことも含めて学習する方が理解が深まりますので、ぜひ、お付き合いください。
エントロピーとは日本語で言うと「乱雑さの度合い」です。日常用語にもなっていて、「部屋が散らかっている」ことを「エントロピーが大きい部屋(@_@;」と表現します。また、情報理論の分野でもエントロピーという用語が使われていて、それが機械学習の分野にも応用されています。
エントロピーはentropyと綴ります。ギリシャ語由来の造語です。多くの人にとってギリシャ語は馴染みのない言語だと思いますので、理解の助けにならない説明ですが…
さて、そんなエントロピーが「説明しにくい物理量」と言われるのは、定義が2つあることが理由です。熱力学での定義と統計力学での定義があります。逆に考えると、同じ物理量に対して2種類の定義が必要なほど、説明が難しい物理量ということになります。
まずは熱力学での定義から考えます。
熱力学では、
$$ \Delta S \text{ ≧ } \frac{q}{T} $$
と定義されます。\( \Delta S \)がエントロピー増加量、\( q \)が外界から流入する熱量、\( T \)が温度です。この式のことを「熱力学第二法則」といいます。
日本語でエントロピーは「乱雑さの度合い」と表現します。「乱雑さ」とは熱に関係する現象で、たとえば「熱の効果により液体に垂らしたインクが、液体中でモヤモヤしている状態」を意味します。液体が高温になればなるほど拡散するインクの速度は速くなり、インクが素早く攪拌されるようになります。そのため、原則として、熱が系に供給されればされるほど、エントロピーが増大する、と表現します。
また、「度合い」は温度で割り算している効果を表しています。 インクが液体中でモヤモヤする現象ですが、高温の液体に、さらに少し熱を加えたところで、(熱を追加で加える前から十分な速さで拡散するため)たいして拡散速度が上がったようには感じられません。一方で、とても冷たくして凍りそうな液体に、少し熱を加えると、(冷たい液体では拡散速度が遅いため)拡散速度が急激に速くなったように感じられます。つまり、高温時の熱の追加ではエントロピーの増大量が小さく、低温時の熱の追加ではエントロピーの増大量が大きくなるように調整しているので、「乱雑さの度合い」と表現し、式では温度で割り算します。
この式は不等式です。それは、「熱が加わるとエントロピーが増大したと考える」、しかし「熱の流入以外でエントロピーを増大させることも可能」ということを意味しています。
熱が加わった分だけエントロピーが増大し、その熱を系の外に捨てればエントロピーも元の値に戻るような現象を「可逆過程」といい、等式部分で表現します。つまり
$$ \Delta S = \displaystyle \frac{q_{rev}}{T} $$
となります。この\( q_{rev} \)は可逆過程で系に流入する熱量です。
一方で、熱以外でエントロピーが増大する現象を「不可逆過程」と言います。たとえば、二層構造になっている系を考えます。内側の層にはインクが入っていて、外側の層にはインクはありません。内側と外側を仕切っている壁を取り外します。すると、系全体にインクが広がります。系全体にインクが広がった状態の方が、エントロピーは大きい(乱雑さの度合いが大きい)と表現します。
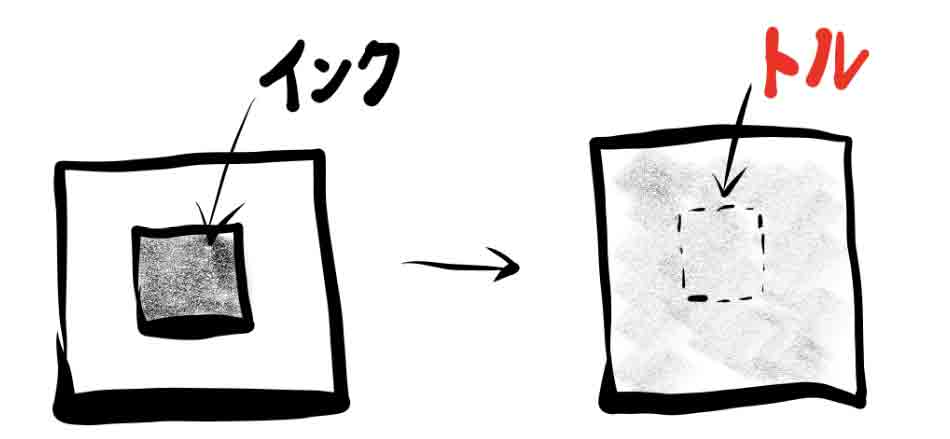
壁を取り払うのに、熱は供給されていませんが、エントロピーは増大しています。つまり、式で表現すると
$$ \Delta S > \displaystyle \frac{q_{irrev}}{T} $$
となります。インクが系全体に拡散した後、壁を元に戻しても、インクは内側の層に戻りません。そのため、この過程は「不可逆過程」と表現します。


コメント