熱力学④　仕事

熱力学第一法則

\( \Delta U = q + w + \mu \Delta N \)

を書き換えるときに以下の2本の式を使用しました。

\(
q = T \Delta S \\
w = – p \Delta V \\
\)

このうち、上の式の \( q \) は熱で、\( w \) が「仕事」です。

ところで、そもそも「仕事」は力学で定義された量です。
運動方程式 \( F = ma \) を位置で積分した、以下の式の、

\( \displaystyle \int_{x_0}^{x_1} F dx = \int_{x_0}^{x_1} ma dx \)

左辺が「仕事」です。

仕事は、力を加えて物を移動させたときの「加えた力の総量」に関連する量です。
仕事が大きければ、その分、物の勢いを示す「運動エネルギー」が増加します。

力を加えて移動させる行為が、熱力学でいうところの「圧縮」に相当します。

では、

\( \displaystyle \int_{x_0}^{x_1} F dx \)

が、

\( – P \Delta V \)

になることを示します。つまり、「力」を加えて「移動させる」行為と、「圧力」を加えて「体積変化させる」行為が一緒であることを示します。

以下のようなピストンを考えます。

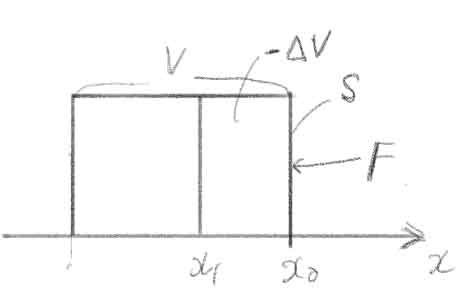
体積が \( V \) 、断面積が \( S \) です。
このピストンの右面の壁を力 \( F \) （圧力 \( P \) ）で押して、内部の気体を圧縮します。
圧力は「単位面積当たりに加わる力」なので、\( F = P \times S \) です。

右面の壁は、\( x_0 \) から \( x_1 \) まで移動します。
ピストン全体の体積は \( V \) ですが、圧縮された領域 \( – \Delta V \) は \( – \Delta V = S \times \left( x_1 – x_0 \right) \) です。マイナスが付くのは圧縮だからです。ピストンの中の体積を \( V \) として、その変化量は、体積が増加する方向で正、減少する方向で負になります。

以上より、

\begin{eqnarray}
\displaystyle \int_{x_0}^{x_1} F dx &=& \int_{x_0}^{x_1} P \times S dx \\
\displaystyle &=& \left[ P \times S \times x \right]_{x_0}^{x_1} \\
\displaystyle &=& P \times S \times \left( x_1 – x_0 \right) \\
&=& P \left( – \Delta V \right) \\
&=& – P \Delta V
\end{eqnarray}

となります。